Cylinder Sphere Packing

Sphere packing in a cylinder is a three-dimensional packing problem with the objective of packing a given number of identical spheres inside a cylinder of specified diameter and length. For cylinders with diameters on the same order of magnitude as the spheres, such packings result in what are called columnar structures.

These problems are studied extensively in the context of biology, nanoscience, materials science, and so forth due to the analogous assembly of small particles (like cells and atoms) into cylindrical crystalline structures.

Appearance in science

Columnar structures appear in various research fields on a broad range of length scales from metres down to the nanoscale. On the largest scale, such structures can be found in botany where seeds of a plant assemble around the stem. On a smaller scale bubbles of equal size crystallise to columnar foam structures when confined in a glass tube. In nanoscience such structures can be found in man-made objects which are on length scales from a micron to the nanoscale.

Botany

Columnar structures were first studied in botany due to their diverse appearances in plants. D'Arcy Thompson analysed such arrangement of plant parts around the stem in his book "On Growth and Form" (1917). But they are also of interest in other biological areas, including bacteria, viruses, microtubules, and the notochord of the zebra fish.

One of the largest flowers where the berries arrange in a regular cylindrical form is the titan arum. This flower can be up to 3m in height and is natively solely found in western Sumatra and western Java.

On smaller length scales, the berries of the ''Arum maculatum'' form a columnar structure in autumn. Its berries are similar to that of the corpse flower, since the titan arum is its larger relative. However, the cuckoo-pint is much smaller in height (height ≈ 20 cm). The berry arrangement varies with the stem to berry size.

Another plant that can be found in many gardens of residential areas is the Australian bottlebrush. It assembles its seed capsules around a branch of the plant. The structure depends on the seed capsule size to branch size.

Foams

A further occurrence of ordered columnar arrangement on the macroscale are foam structures confined inside a glass tube. They can be realised experimentally with equal-sized soap bubbles inside a glass tube, produced by blowing air of constant gas flow through a needle dipped in a surfactant solution. By putting the resulting foam column under forced drainage (feeding it with surfactant solution from the top), the foam can be adjusted to either a dry (bubbles shaped as polyhedrons) or wet (spherical bubbles) structure.

Due to this simple experimental set-up, many columnar structures have been discovered and investigated in the context of foams with experiments as well as simulation. Many simulations have been carried out using the Surface Evolver to investigate dry structure or the hard sphere model for the wet limit where the bubbles are spherical.

In the zigzag structure the bubbles are stacked on top of each other in a continuous w-shape. For this particular structure a moving interface with increasing liquid fraction was reported by Hutzler ''et al.'' in 1997. This included an unexpected 180° twist interface, whose explanation is still lacking.

The first experimental observation of a line-slip structure was discovered by Winkelmann ''et al.'' in a system of bubbles.

Further discovered structures include complex structures with internal spheres/foam cells. Some dry foam structures with interior cells were found to consist of a chain of pentagonal dodecahedra or Kelvin cells in the centre of the tube. For many more arrangements of this type, it was observed that the outside bubble layer is ordered, with each internal layer resembling a different, simpler columnar structure by using X-ray tomography.

Nanoscience

Columnar structures have also been studied intensively in the context of nanotubes. Their physical or chemical properties can be altered by trapping identical particles inside them. These are usually done by self-assembling fullerenes such as C60, C70, or C78 into carbon nanotubes, but also boron nitride nanotubes

Such structures also assemble when particles are coated on the surface of a spherocylinder as in the context of pharmaceutical research. Lazáro ''et al.'' examined the morphologies of virus capsid proteins self-assembled around metal nanorods. Drug particles were coated as densely as possible on a spherocylinder to provide the best medical treatment.

Wu ''et al.'' built rods of the size of several microns. These microrods are created by densely packing silica colloidal particles inside cylindrical pores. By solidifying the assembled structures the microrods were imaged and examined using scanning electron microscopy (SEM).

Columnar arrangements are also investigated as a possible candidate of optical metamaterials (i.e. materials with a negative refractive index) which find applications in super lenses or optical cloaking. Tanjeem ''et al.'' are constructing such a resonator by self-assembling nanospheres on the surface of the cylinder. The nanospheres are suspended in an SDS solution together with a cylinder of diameter $D$, much larger than the diameter of the nanospheres $d$ ($D/d \approx 3 \text 5$). The nanospheres then stick to the surface of the cylinders by a depletion force.

Classification using phyllotactic notation

The most common way of classifying ''ordered'' columnar structures uses the phyllotactic notation, adopted from botany. It is used to describe arrangements of leaves of a plant, pine cones, or pineapples, but also planar patterns of florets in a sunflower head. While the arrangement in the former are cylindrical, the spirals in the latter are arranged on a disk. For columnar structures phyllotaxis in the context of cylindrical structures is adopted.

The phyllotactic notation describes such structures by a triplet of positive integers $(l = m+n, m, n)$ with $l \geq m \geq n$. Each number $l$, $m$, and $n$ describes a family of spirals in the 3-dimensional packing. They count the number of spirals in each direction until the spiral repeats. This notation, however, only applies to triangular lattices and is therefore restricted to the ordered structures without internal spheres.

Types of ordered columnar structures without internal spheres

Ordered columnar structures without internal spheres are categorised into two separate classes: ''uniform'' and ''line-slip'' structures. For each structure that can be identified with the triplet $(l, m, n)$, there exist a uniform structure and at least one line slip.

Uniform structure

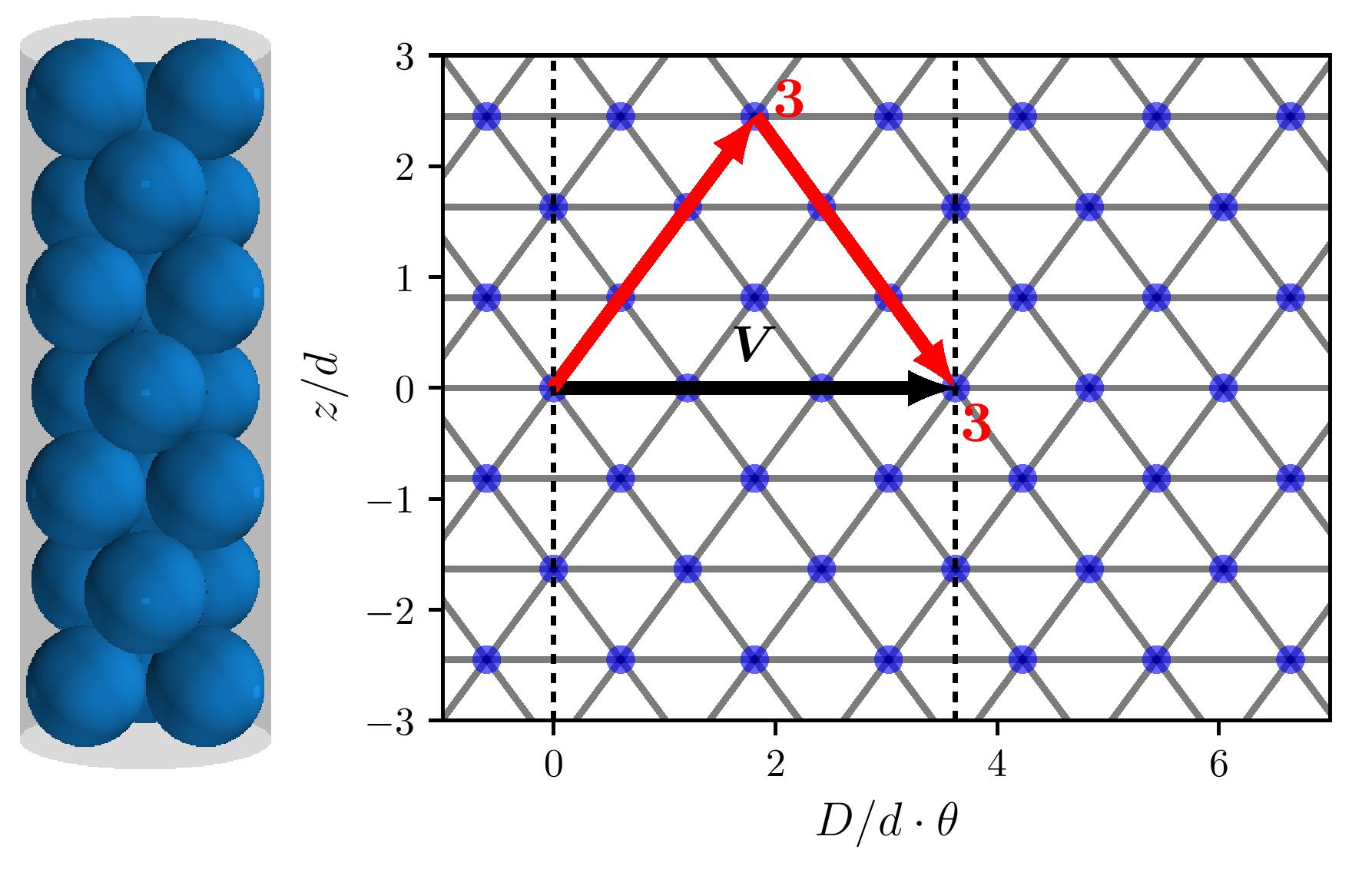
A uniform structure is identified by each sphere having the same number of contacting neighbours. This gives each sphere an identical neighbourhood. In the example image on the side each sphere has six neighbouring contacts.

The number of contacts is best visualised in the rolled-out contact network. It is created by rolling out the contact network into a plane of height $z$ and azimuthal angle $\theta$ of each sphere. For a uniform structure such as the one in the example image, this leads to a regular hexagonal lattice. Each dot in this pattern represents a sphere of the packing and each line a contact between adjacent spheres.

For all uniform structures above a diameter ratio of $D/d > 2.0$, the regular hexagonal lattice is its characterising feature since this lattice type has the maximum number of contacts. For different uniform structures $(l, m, n)$ the rolled-out contact pattern only varies by a rotation in the $z \text\theta$ plane. Each uniform structure is thus distinguished by its periodicity vector $V$, which is defined by the phyllotactic triplet $(l, m, n)$.

Line-slip structure

For each uniform structure, there also exists a related but different structure, called a line-slip arrangement.

The differences between uniform and line-slip structures are marginal and difficult to spot from images of the sphere packings. However, by comparing their rolled-out contact networks, one can spot that certain lines (which represent contacts) are missing.

All spheres in a uniform structure have the same number of contacts, but the number of contacts for spheres in a line slip may differ from sphere to sphere. For the example line slip in the image on the right side, some spheres count five and others six contacts. Thus a line slip structure is characterised by these gaps or loss of contacts.

Such a structure is termed line slip because the losses of contacts occur along a line in the rolled-out contact network. It was first identified by Picket ''et al.'', but not termed line slip.

The direction, in which the loss of contacts occur can be denoted in the phyllotactic notation $(l, m, n)$, since each number represents one of the lattice vectors in the hexagonal lattice. This is usually indicated by a bold number.

By shearing the row of spheres below the loss of contact against a row above the loss of contact, one can regenerate two uniform structures related to this line slip. Thus, each line slip is related to two adjacent uniform structures, one at a higher and one at a lower diameter ratio $D/d$.

Winkelmann ''et al.'' were the first to experimentally realise such a structure using soap bubbles in a system of deformable spheres.

Dense sphere packings in cylinders

Columnar structures arise naturally in the context of dense hard sphere packings inside a cylinder. Mughal ''et al.'' studied such packings using simulated annealing up to the diameter ratio of $D/d = 2.873$ for cylinder diameter $D$ to sphere diameter $d$. This includes some structures with internal spheres that are not in contact with the cylinder wall.

They calculated the packing fraction for all these structures as a function of the diameter ratio. At the peaks of this curve lie the uniform structures. In-between these discrete diameter ratios are the line slips at a lower packing density. Their packing fraction is significantly smaller than that of an unconfined lattice packing such as fcc, bcc, or hcp due to the free volume left by the cylindrical confinement.

The rich variety of such ordered structures can also be obtained by sequential depositioning the spheres into the cylinder. Chan reproduced all dense sphere packings up to $D/d < 2.7013$ using an algorithm, in which the spheres are placed sequentially dropped inside the cylinder.

Mughal ''et al.'' also discovered that such structures can be related to disk packings on a surface of a cylinder. The contact network of both packings are identical. For both packing types, it was found that different uniform structures are connected with each other by line slips.

Fu ''et al.'' extended this work to higher diameter ratios $D/d < 4.0$ using linear programming and discovered 17 new dense structures with internal spheres that are not in contact with the cylinder wall.

A similar variety of dense crystalline structures have also been discovered for columnar packings of spheroids through Monte Carlo simulations. Such packings include achiral structures with specific spheroid orientations and chiral helical structures with rotating spheroid orientations.

Columnar structures created by rapid rotations

A further dynamic method to assemble such structures was introduced by Lee ''et al''. Here, polymeric beads are placed together with a fluid of higher density inside a rotating lathe.

When the lathe is static, the beads float on top of the liquid. With increasing rotational speed, the centripetal force then pushes the fluid ''outwards'' and the beads ''toward'' the central axis. Hence, the beads are essentially confined by a potential given by the rotational energy$E_ = \frac m R^2 \omega^2,$where $m$ is the mass of the beads, $R$ the distance from the central axis, and $\omega$ the rotational speed. Due to the $R^2$ proportionality, the confining potential resembles that of a cylindrical harmonic oscillator.

Depending on number of spheres and rotational speed, a variety of ordered structures that are comparable to the dense sphere packings were discovered.

A comprehensive theory to this experiment was developed by Winkelmann ''et al.'' It is based on analytic energy calculations using a generic sphere model and predicts peritectoid structure transitions.

See also

* Sphere packing
* Close-packing of equal spheres
* Packing problems

References

External links

* Becker, Aaron T. and Huang, L.
"Packing spheres into a Thin Cylinder"
''MathWorld''.
{{Packing problems

Packing problems
Spheres
Discrete geometry
Crystallography